گروه Group

گروه Group
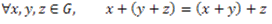
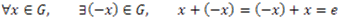
ساختار جبری (+,G) را یک گروه گوییم هرگاه در شرایط زیر صدق کند:

سه شرط اول در پست های قبل توضیح داده شد. شرط چهارم یعنی هر عضو یک گروه دارای قرینه است.

به عبارتی می توان گفت هر تکوار که هر عضو آن دارای قرینه باشد یک گروه است.

مثال های فراوانی برای گروه ها وجود دارد که ان شاالله به مرور در همین پست قرار داده می شوند.
برای این منظور کافی است یک مجموعه با یک عمل را درنظر بگیریم و بررسی کنیم که آیا عمل تعریف شده روی این مجموعه در چهار شرط بالا صدق می کنند یا نه.

تذکر:عضو قرینه در یک گروه، لزوما با قرار دادن یک منفی پشت عنصر حاصل نمی شود. علامت منفی در اینجا صرفا برای درک بهتر عنصر قرینه است، می توان به جای این نماد از نماد دیگری برای نمایش عنصر قرینه استفاده کرد.