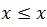مشبکه کراندار Bounded Lattice

مشبکه کراندار Bounded Lattice

ساختار جبریرا مشبکه ای کراندار گوییم هرگاهیک مشبکه باشد و عضوهای 0 و 1 در L در شرایط زیر صدق کنند:

                                             

                                             

0 را کران پایین و 1 را کران بالای L می نامیم.

مثال: مشبکه زیر، مشبکه ای کراندار است. کران پایین و بالای آن را مشخص کنید.

                                                

مشبکه Lattice

مشبکه Lattice

مجموعه ی مرتب جزئی L همراه با عمل دوتایی  ≥  را یک مشبکه (Lattice) گوییم هرگاه برای هر دو عضو x و y از L، بزرگترین کران پایین {x,y} و کوچکترین کران بالای {x,y} موجود باشد.

یعنی:

به عبارتی می‌توان گفت، L یک مشبکه است هرگاه یک رسند-نیم مشبکه و یک وست-نیم مشبکه باشد.

می توان مشبکه را به صورت جبری نیز تعریف کرد.

جبر (L; ∨,∧) را یک مشبکه نامیم هرگاه در شرایط زیر صدق کند:

1)     خودتوانی:

جا به جایی:

شرکت پذیری:

1)     جذب:

مثال: مجموعه ی توانی همراه با عمل اشتراک و اجتماع یک مشبکه است.

زیرا به وضوح خواص خودتوانی، جا به جایی، شرکت پذیری و خاصیت جذب برای اجتماع و اشتراک مجموعه ها برقرار است.

برای درک بهتر، فرض کنیم مجموعه X برابر باشد با:

بنابراین:

نمودار هاسه این مشبکه به شکل زیر است:

نیم مشبکه Semilattice

 نیم مشبکه Semilattice

 مجموعه ی مرتب جزئی S همراه با عمل دوتایی ≥ را یک رسند-نیم مشبکه (meet-semilattice) گوییم هرگاه برای هر دو عضو x و y از S بزرگترین کران پایین (Greatest Lower Bound) {x,y} موجود باشد.

 بزرگترین کران پایین {x,y} را با inf{x,y} یا x˄y نمایش می دهیم.

 به همین ترتیب وست-نیم مشکبه را تعریف می کنیم.

 در وست-نیم مشبکه (join-semilattice)، به ازای هر دو عضو x و y از S، کوچکترین کران بالای (Least Upper Bound) {x,y} موجود است.

 کوچکترین کران بالای {x,y} را با sup{x,y} یا x˅y نمایش می دهیم.

 

 می توانیم تعریفی جبری از نیم مشبکه ارائه دهیم.

 برای این منظور مجموعه ی S را همراه با عمل دوتایی ˄ در نظر می گیریم به طوریکه  شرایط زیر برقرار باشد:

x˄x=x

x˄y=y˄x

x˄(y˄z)=(x˄y)˄z

 در این صورت S را رسند-نیم مشبکه گویند.

 و به همین نحو وست-نیم مشبکه تعریف می شود.

 مثال:

                                                       

 این نمودار هاسه، نمایش دهنده ی یک رسند-نیم مشبکه (و وست-نیم مشبکه) است. زیرا meet (و join) هر دو عضو موجود است و شرایط ذکر شده در بالا برقرار است:

 به وضوح دو شرط اول برقرارند. شرط سوم را بررسی می کنیم:

a˄(b˄c) = a˄a = a

(a˄b)˄c = a˄c = a

 پس دو طرف تساوی با هم برابرند. با بررسی شرط سوم بر تک تک عناصر، نیم مشبکه بودن نمودار فوق، بدست می‌آید.

 

سوال: نشان دهید شکل زیر هیچ یک از انواع نیم مشبکه نیست.

                                            

نکته: با رابطه ی زیر می توان نشان داد دو تعریف فوق (تعریف ترتیبی و تعریف جبری) از نیم مشبکه با هم معادلند:

x ≤ y ↔ x˅y=y

x ≤ y ↔ x˄y=x

 

مرور بر مطالب قبل:

                                                           

نمودار هاسه Hasse Diagram

 نمودار هاسه Hasse Diagram

 فرض کنید (A,≤) یک مجموعه ی مرتب جزئی باشد. نمودار هاسه این مجموعه به صورت زیر ساخته می‌شود:

1.      به ازای هر یک از اعضای A یک نقطه در صفحه در نظر می‌گیریم. اگر a و b دو عضو متمایز از A باشند که a≤b ارتفاع b بیشتر از a باشد.

2.      اگر a و b دو عضو متمایز باشند و a≤b آنگاه با یک منحنی صعودی نقطه نظیر a را به نقطه نظیر b وصل می‌کنیم.

3.      تمام منحنی‌های رسم شده در گام 2 را برای خواص تعدی حذف می‌کنیم.

یعنی اگر a≤b نقطه نظیر a را به نقطه نظیر b با یک منحنی وصل می‌کنیم هرگاه عنصر c متمایز از a و b نداشته باشیم که a≤c≤b.

مثال: زوج های مرتب روی مجموعه اعداد طبیعی را با رابطه ی زیر در نظر بگیریم:

  (a,b) ≤ (c,d) if a ≤ c and b ≤d                                                                          

  نمودار هاسه به شکل زیر خواهد بود:

                                           

توجه1: برای رسم نمودار هاسه روش های متعددی وجود دارد، اما معمولا برای رسم ابتدا نقطه مینیمم (در صورت وجود) را قرار می دهند و باتوجه به رابطه ترتیب، نقاط و خطوط دیگر را اضافه می کنند. بنابراین نمودار هاسه هر مجموعه مرتب جزئی یکتا نیست.

توجه2: در نمودار هاسه دور و طوقه وجود ندارد. (با توجه به الگوریتم رسم واضح است.)

مجموعه ی مرتب جزئی Partial Order Set

مجموعه مرتب جزئی Partial Order Set (poset)

رابطه ی ≥  را مرتب جزئی گوییم هرگاه به ازای هر x و y و z در A داشته باشیم:

خودتوان باشد:

پادتقارنی باشد:

تعدی باشد:

مجموعه ی A همراه با رابطه ترتیب ≥ را مجموعه مرتب جزئی گوییم.

مثال: مجموعه ی اعداد طبیعی همراه با رابطه ی عاد کردن، مجموعه ای جزئی مرتب است.

 

اگر هر دو عضو در مجموعه ی A قابل مقایسه باشند، آنگاه مجموعه A را کلی مرتب (Total Order) می نامیم. به عبارتی به ازای هر x و y در A، داشته باشیم:

مثال: مجموعه ی اعداد طبیعی با رابطه ی ترتیب معمولی، مجموعه ای کلی مرتب است.

مثال: عاد کردن رابطه ای کلی مرتب نیست، زیرا مثلا 2 و 3 هیچ یک برهم بخش پذیر نیستند، بنابراین در رابطه ی عاد کردن صدق نمی کنند.