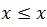مجموعه مرتب جزئی Partial Order Set (poset)
رابطه ی ≥ را مرتب جزئی گوییم هرگاه به ازای هر x و y و z در A داشته باشیم:
مجموعه ی A همراه با رابطه ترتیب ≥ را مجموعه مرتب جزئی گوییم.
مثال: مجموعه ی اعداد طبیعی همراه با رابطه ی عاد کردن، مجموعه ای جزئی مرتب است.
اگر هر دو عضو در مجموعه ی A قابل مقایسه باشند، آنگاه مجموعه A را کلی مرتب (Total Order) می نامیم. به عبارتی به ازای هر x و y در A، داشته باشیم:
مثال: مجموعه ی اعداد طبیعی با رابطه ی ترتیب معمولی، مجموعه ای کلی مرتب است.
مثال: عاد کردن رابطه ای کلی مرتب نیست، زیرا مثلا 2 و 3 هیچ یک برهم بخش پذیر
نیستند، بنابراین در رابطه ی عاد کردن صدق نمی کنند.
- ۰ نظر
- ۲۱ دی ۹۴ ، ۱۲:۵۲
- ۳۴۴۵ نمایش